Créer une fonction permet d'éviter de copier-coller un ensemble de lignes de code, en généralisant leur exécution avec un système de paramètres et de valeur de retour. À chaque appel de la fonction, on pourra lui donner de nouveaux paramètres ce qui pourra modifier la valeur retournée par la fonction.

​

Une fonction se définie avec le mot clé def :

def nom_fonction(param1,param2,...,param_n):

    actions

​

Une fonction peut retourner une ou plusieurs valeurs avec le mot clé return. Sachez qu'après un return, on sort de la fonction. Si la fonction n'a pas de return, elle renverra None.

On peut écrire plusieurs return, par exemple, on pourrait avoir un return pour chacune des conditions de la fonction.

​

Exemple d'une fonction renvoyant le carré de la variable passée en paramètre :

def carre(x):

    return x*x

​

Pour appeler une fonction, il suffit juste de la nommer et d'indiquer dans les parenthèses les paramètres nécessaires.

carre(5) # Renvoie 25 

​

​

​

Les fonctions lambda sont des fonctions plus simples que celles définies avec le mot clé def. Elles se définissent en une ligne et ne possède pas de mot clé return. 

 

Pour les définir il faut utiliser le mot clé lambda :

mult = lambda x, y : x*y # Fonction lambda renvoyant le produit de deux nombres passés en paramètre

mult(3,2) # Utilisation comme une fonction classique. Renvoie 6.

​

test = lambda val : print('pair') if val % 2 == 0 else print('impair') # Fonction lambda affichant pair ou impair selon la parité du paramètre val

test(3) # Utilisation comme une fonction classique. Affiche impair.

​

​

Il est intéressant d'utiliser les fonctions lambda avec la fonction filter. En effet, la fonction filter admet deux paramètres : une fonction et un itérable (une liste par exemple). Elle permet de garder seulement les éléments de l'itérable pour lesquels la fonction passée en paramètre renvoie True.

La fonction filter renvoie un itérable, on peut donc l'utiliser dans un for. On peut aussi obtenir la liste filtrée avec une compréhension de liste.

​

liste = [1,2,3,4,5,6,7,8,9]

lambda val : True if val%2==0 else False # On utilisera pour l'exemple cette fonction lambda qui garde seulement les valeurs paires de la liste

​

Utilisation dans un for :

for element in filter(lambda val : True if val%2==0 else False, liste): # On peut aussi créer préalablement un objet filter pour simplifier l'écriture du for

    actions

​

Obtention de la liste filtrée :

liste_paire = [element for element in filter(lambda val : True if val%2==0 else False, liste)]

​

​

​

Enfin, parlons maintenant des fonctions récursives qui sont des fonctions particulières. En effet, les fonctions récursives sont des fonctions dont leurs actions nécessitent d'invoquer la fonction elle-même.

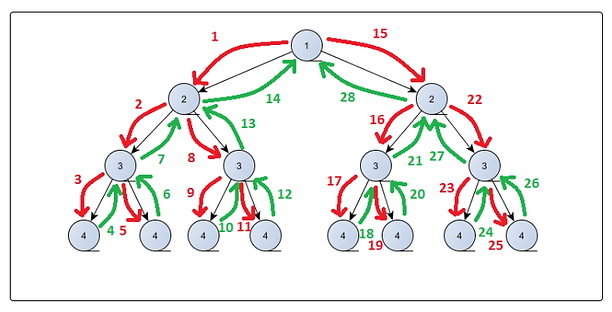
L'exécution d'une fonction récursive se fait sous la forme d'un arbre dont la racine est le premier appel de la fonction. À chaque appel de la fonction, on descend plus profondément dans l'arbre jusqu'à arriver à une feuille (flèches rouges dans le schéma ci-dessous).

Dès que la feuille a renvoyé une valeur, on remonte jusqu'à un nœud dont la valeur n'est pas calculée. On calcule ensuite la valeur du nœud en descendant dans l'arbre jusqu'à arriver à une autre feuille. On répète ces actions jusqu'à parcourir tout l'arbre de gauche à droite.

Ainsi la dernière valeur qui sera retournée correspond au return de fin du tout premier appel de la fonction récursive (le numéro 28 en vert du schéma ci-dessous).

​

L'exécution d'une feuille est appelé le cas de base, c'est le seul cas où le return ne retournera pas la fonction mais une constante (comme un des paramètres par exemple). C'est ce qui permet de remonter dans l'arbre (flèches vertes ci-dessous).

​

Voici un schéma pour comprendre un peu mieux l'exécution d'une fonction récursive :

​

​

​

​

​

​

​

​

​

​

​

​

​

​

Exemple d'une fonction récursive calculant x à la puissance y :

def power(x, y):

    if y == 1: # Cas de base : on atteint la feuille

        return x # On retourne x. C'est à partir de là que la fonction va remonter dans l'arbre  d'exécution.

    if y % 2 == 0: # Si y est pair

        x_2 = power(x, y//2) # L’intérêt des appels de la fonction récursive est de changer la valeur des paramètres

        return x_2 ** 2

    return x * power(x, y-1)

​

Exemple d'une fonction récursive trouvant le PGCD entre deux nombres :

def pgcd(n, p):

    if n == p: # Cas de base : on atteint la feuille

        return n # On retourne n. C'est à partir de là que la fonction va remonter dans l'arbre  d'exécution.

    if n > p: # On utilise if et non elif car le return du if précédent arrête l'exécution 

        return pgcd(n-p, p) # On diminue n jusqu'à ce que n=p

    else:

        return pgcd(n, p-n) # On diminue p jusqu'à ce que n=p